Research Highlights
Turbulent cascades and phase dynamics
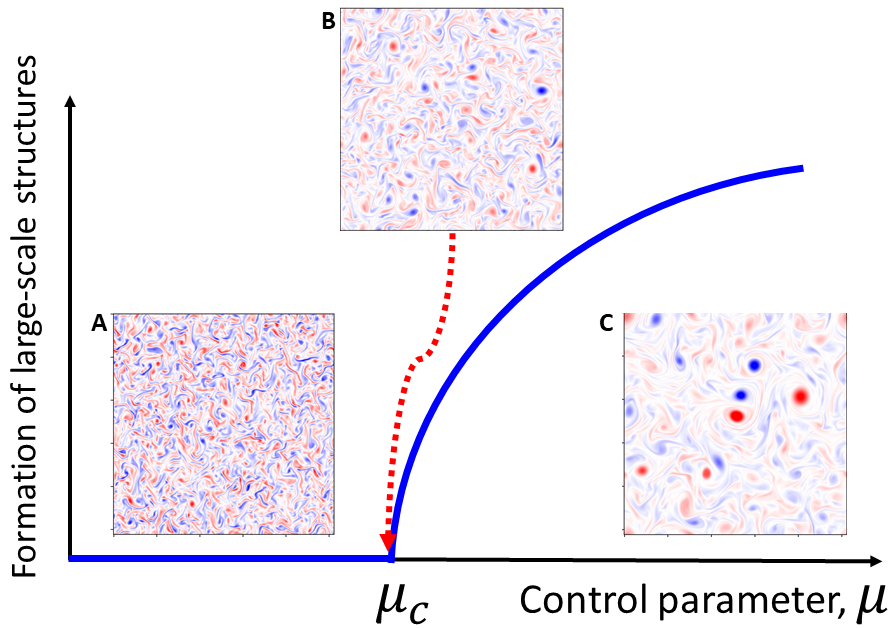
Turbulence—the chaotic motion of fluids—acts to transport and mix energy, momentum, and other material properties in many systems of interest, ranging from pipe flows to Jupiter’s atmosphere. Turbulence is not just chaotic but also multi-scale, and the transfer (or ‘cascade’) of energy across scales is a central aspect of turbulent flows. It determines the size and lifetime of flow structures, which in turn affect transport and mixing. Despite its central role in the few predictive turbulence theories that exist, a dynamical understanding of what determines the cascade of energy (and its direction in scale) has yet to be established. This is particularly evident in geophysical and astrophysical flows, where the energy cascade can have a variety of unexplained behaviors depending on parameters such as rotation rate or aspect ratio.
My work aims to study the statistics of energy transfers and cascades in turbulent flows using a combination of direct numerical simulations, simplified numerical models of turbulence, and stochastic models. Recently, I have focused on the role that so-called ‘triads’ (the interaction of flow structures at three different scales) play in the energy cascade. Triads can be regarded as the smallest dynamical system representing cascade dynamics. Triads have two properties associated with them, an energy and a phase (much like a Cosine wave has an amplitude and a phase). While the former has been central to the last century of turbulence theory, I believe that the latter has been overlooked, and is an ongoing focus of my work.
Transition to turbulence and wall-bounded shear flows
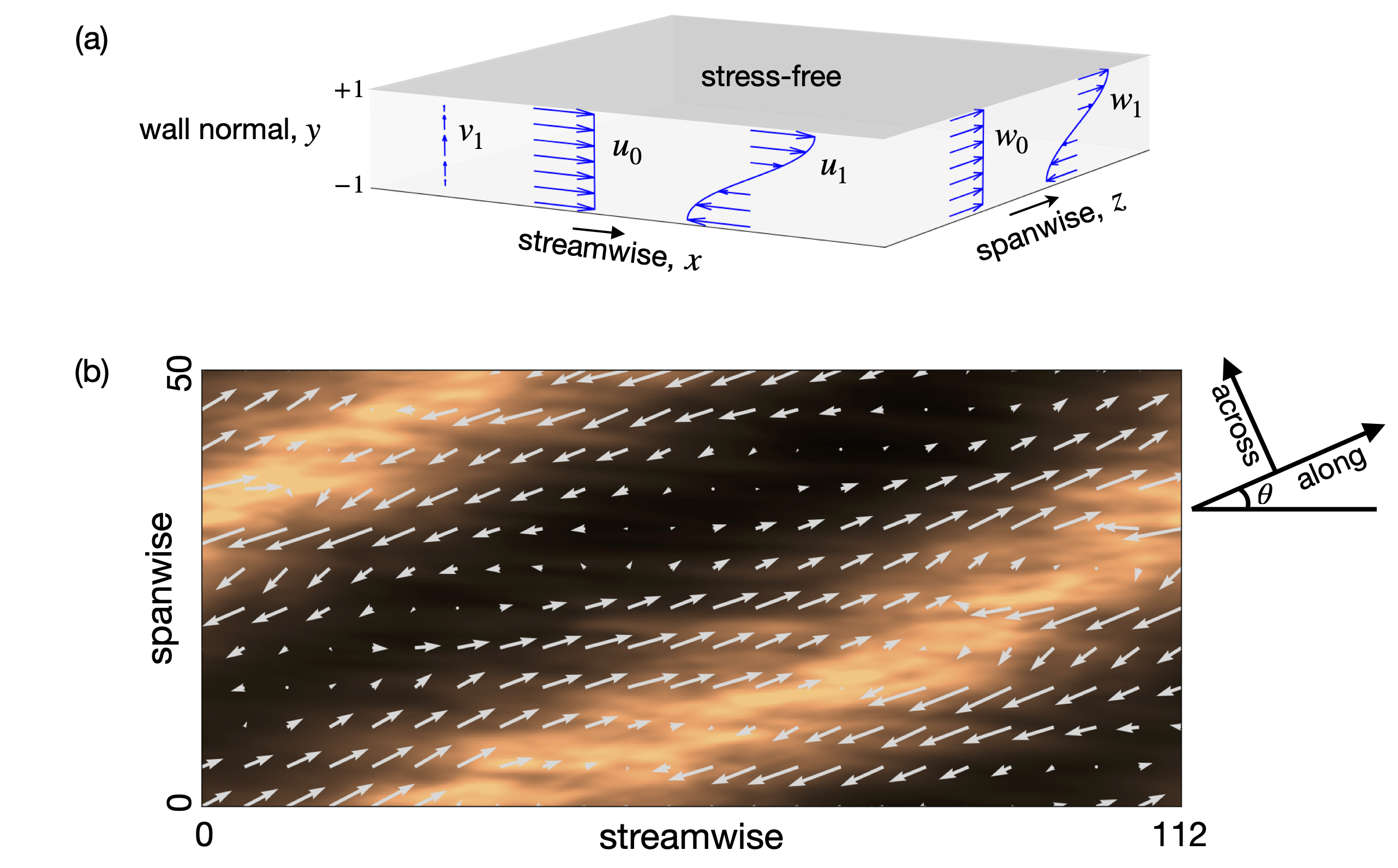
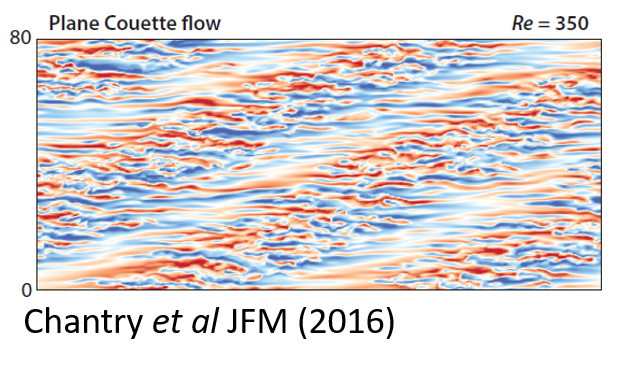
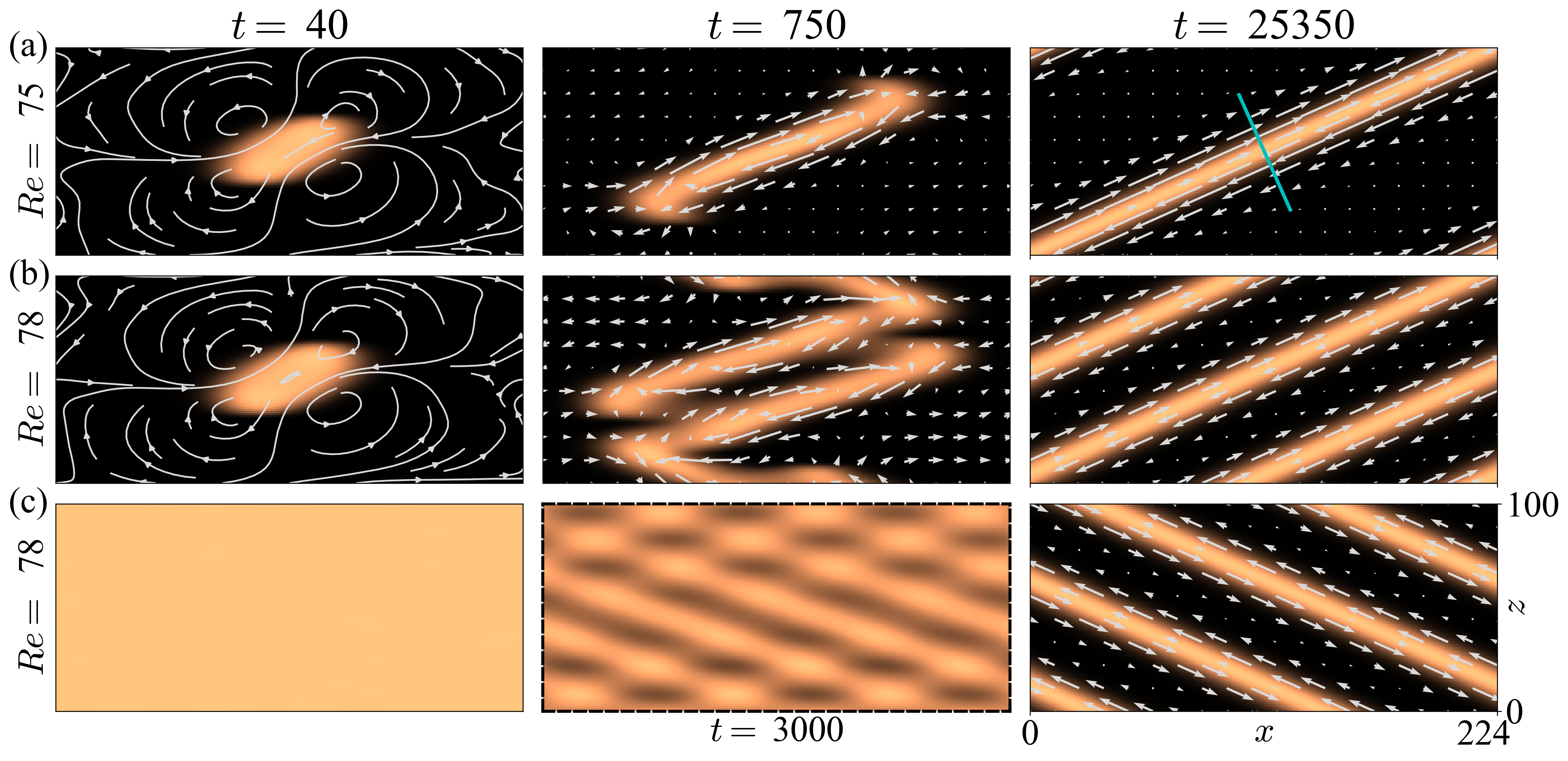
The transition from simple laminar flow to the chaotic, multiscale turbulent state remains one of the great open problems in fluid dynamics. It involves elements of nonlinear dynamics, bifurcation theory, pattern formation, and non-equilibrium phase transitions. What is particularly fascinating is that, in simple flows such as pipes and channels, the transition to turbulence is subcritical: laminar flow remains linearly stable to perturbations, and yet turbulence arises through the local proliferation of large-scale turbulent patches within the domain. In flows between parallel walls, this gives rise to striking phenomena featuring oblique turbulent–laminar patterns (or ‘bands’), whose geometry and dependence on flow speed are not yet understood.
My work aims to improve the understanding and modelling of the transition to turbulence in planar shear flows through a combination of direct numerical simulations and simplified mathematical modelling. My recent work has focused on the development and analysis of a coarse-grained (large-scale) model of the transition to turbulence in Waleffe flow, an analogue of plane Couette flow. This model describes the dynamics of the large-scale quasi-laminar flow and turbulence, and provides both numerical and analytical advantage to a full direct numerical simulation. It is able to reproduce the observed transitional phenomena, namely oblique turbulent-laminar patterns, and opens the door to a physical understanding of the mechanisms at play.
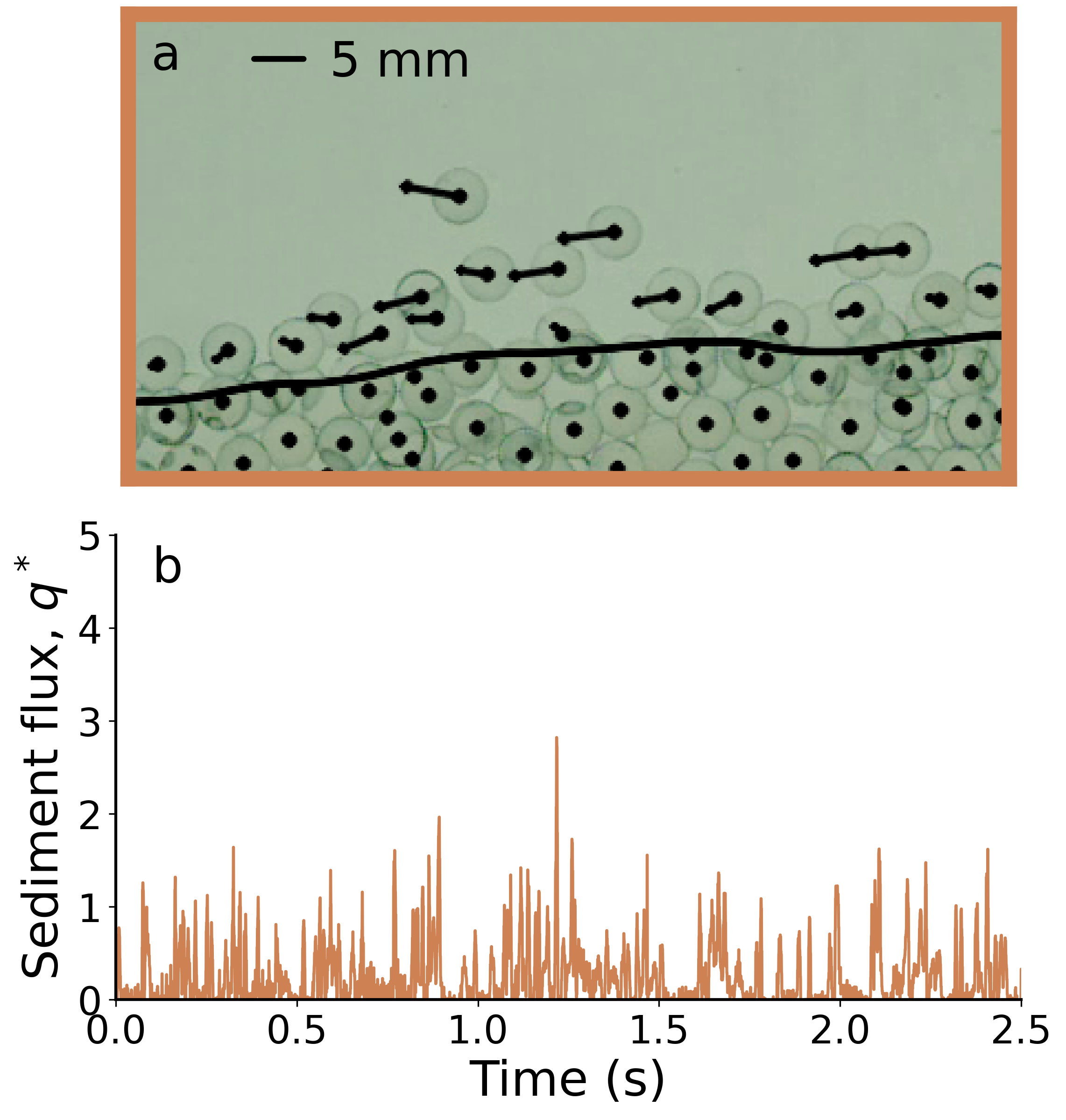
Sediment transport
In bed load sediment transport, grains are moved by turbulent flow and are in nearly continuous contact with other grains. Despite their chaotic and unpredictable trajectories, each individual grain ultimately contributes to the ordered, large-scale properties of the river they are a part of - from the way it transports sediment to its width and shape. However, connecting the time and length scales of grain motion and river evolution is challenging in both experimental and numerical settings.
My work aims to understand the connection from grain to river scales using a series of intermediate-complexity models and simplified statistical approaches. My past work has focused on simple stochastic models describing intermittent sediment flux time series observed in the field and laboratory experiments [1,2]. More recently, I've developed a cellular automaton model of grain dynamics based around the concept of collective entrainment, which can reproduce intermittent statistics in both time and space, as well as describe channel-scale bank evolution. The simplicity of this model opens the door for both analytical and numerical analysis of sediment transport statistics and channel evolution.